Лекция 16. Основы математического планирования эксперимента

Планирование эксперимента - раздел математической статистики, изучающий рациональную организацию измерений, подверженных случайным ошибкам.

Под экспериментом здесь подразумевается следующее:

Эксперимент - изучение зависимости целевой функции (или функции отклика) y от нескольких факторов x₁ ... x_n

Цели планирования эксперимента:

1. Теоретические: изучение характера зависимости, степень влияния различных факторов на целевую функцию, предсказание значения целевой функции при определенных значениях факторов.

2. Практические: поиск оптимальных условий (набора значений факторов), при которых целевая функция достигает экстремума (минимума или максимума). Например: поиск условий измерения, чтобы погрешность была минимальна. Или: оптимизация условий хроматографического разделения для достижения максимального разрешения пиков.

Разберем подходы к планированию эксперимента на примере поиска оптимальных условий измерения в атомно-абсорбционном методе. В качестве целевой функции возьмем оптическую плотность (y), а в качестве факторов - температуру атомизатора (x₁) и концентрацию модификатора матрицы (x₂). Будем искать условия (значения факторов) при которых оптическая плотность достигает максимума.

Общий вид зависимости целевой функции от параметров x₁ и x₂ приведен на рисунке:

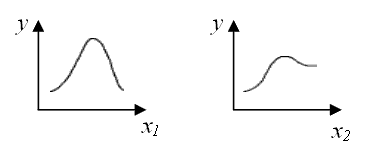
Как видно из рисунка, обе зависимости имеют максимум, а не возрастают монотонно. Поэтому важна задача оптимизации.

Зависимость целевой функции одновременно от двух факторов можно изобразить в виде "контурной карты" (это вид сверху на трехмерную поверхность отклика, описывающую функцию y):

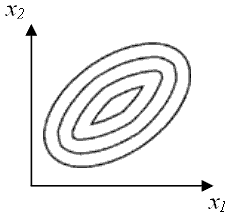
Отметим, что в данном случае наблюдается совместное влияние факторов x₁ и x₂ (т.е. корреляция между факторами). Поэтому традиционный эксперимент (когда варьируют один параметр, ищут максимум, затем варьируют другой параметр и также ищут максимум) не подходит - максимум таким образом не найти (или придется много раз по очереди варьировать параметры). Вот к чему приведет традиционный эксперимент (красной точкой отмечен ошибочно найденный максимум функции отклика):

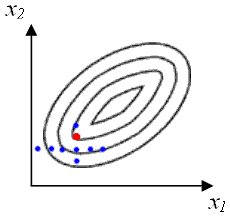
Вывод: необходимо варьировать одновременно все факторы, и двигаться в направлении возрастания функции:

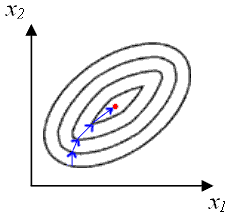
Для решения задачи поиска максимума (минимума) функции отклика существует метод факторного планирования эксперимента, который позволяет получить максимально точное решение за минимальное количество измерений.

лекции читает А.В.Гармаш, химический факультет МГУ